Lucas Lacasa, Queen Mary University of London
Va a un concierto de su banda preferida. En un momento de la noche, el cantante deja al público la labor de entonar. Usted, como los amigos que le acompañan, se desgañita cantando. En mitad de la euforia, se da cuenta de lo mal que lo está haciendo. De hecho, se da cuenta de que todos sus amigos cantan mal. “¡Qué horror!”, piensa.
Un par de días después, entra en YouTube para buscar vídeos del concierto. Para su asombro, la parte en la que canta el público ¡es casi la mejor! Pelos de punta. ¿Cómo puede sonar tan bien? Por un momento se fustiga: “Mis amigos y yo seríamos los únicos que desafinábamos entre las 50.000 personas”. Pero luego piensa: “No, ¿cómo puede ser? Si bien alguien habría que cantase bien, en general la gente desafina”.
Y tiene razón.
Si no ha experimentado de primera mano lo anteriormente descrito, le sugiero que escuche esto:
Y ahora, esto:
Por extraño que parezca, al combinar una gran multitud en la que cada uno canta mal, el cántico colectivo suena coral, afinado. Este efecto puede verse como un ejemplo de inteligencia colectiva, donde el grupo es más eficiente que cada individuo a la hora de realizar una tarea concreta.
Es importante señalar que lo que escuchamos no es solo un efecto de tipo regresión a la media, donde los que desafinan por arriba anularían a los que lo hacen por abajo. Es algo más sutil, un efecto psicoacústico en el que entran en juego la física, la fisiología y la cognición humana.
La misteriosa teoría del tono percibido
Cuando producimos un tono puro, con una única frecuencia, el tono que escuchamos coincide con esa frecuencia. Sin embargo, cuando tocamos a la vez varios tonos puros, ¿cuál es la frecuencia que percibimos? ¿En qué tono suena eso?
La teoría del tono percibido ha sido fuente de debate y controversia desde el siglo XIX. Cuando varios tonos puros se superponen a la vez, la onda sonora resultante se denomina tono complejo. Cada uno de los tonos puros que la componen se denominan parciales.
El tono percibido de un tono complejo es la frecuencia efectiva a la que el oído humano percibe que suena esa onda sonora. Aunque esta es una cantidad medible, no es el resultado de una simple combinación de parciales. Entran en juego no solo la naturaleza de la onda sonora, sino también del oído que la percibe y del circuito cerebral que la procesa.
En ocasiones, el tono percibido no se corresponde con ninguna de las frecuencias de los parciales. Es decir, no existe ni siquiera una vibración física a la frecuencia que se escucha.
Cuando el tono complejo se obtiene por la mezcla de únicamente dos tonos puros con frecuencias f₁ y f₂, entonces suele ser habitual asociar el tono percibido con la frecuencia fundamental, definida como el mayor divisor común de f₁ y f₂. Cuando mezclamos más de dos tonos puros esta receta no siempre funciona.
Hace unas décadas, el físico Eric Heller de la Universidad de Harvard en Estados Unidos estudiaba problemas de espectroscopía molecular. Observó entonces que en el espectro de luminiscencia de algunas moléculas aparecían ciertos patrones vibrónicos fantasma, algo similar a un tono percibido en un contexto donde las señales no son temporales sino espaciales.
Heller, apasionado por la física de la acústica, estudió años después y de forma teórica el problema paralelo de encontrar el tono percibido en un tono complejo, obteniendo un algoritmo para calcularlo basado en estudiar las propiedades de la función de autocorrelación de la señal.
Si todos desafinamos un poco, el tono percibido estará afinado
La clave para entender por qué el cántico del público parece afinado está en estudiar el tono percibido de un tono complejo. Gracias a Heller, ahora tenemos un algoritmo para hacerlo.
El tono complejo estaría compuesto por tantos parciales como personas en el público. Para hacerlo sencillo: si el tono afinado se corresponde con una frecuencia f , podemos modelizar la desafinación de cada miembro del público como f + d, donde d es una variable aleatoria extraída de una distribución Gaussiana de media cero y varianza s².
Al aplicar el algoritmo de Heller al tono complejo que modeliza el cántico del público obtenemos como resultado que el tono percibido es igual a f + s² /f. Como el segundo término es mucho más pequeño que el primero, el tono percibido estará afinado.
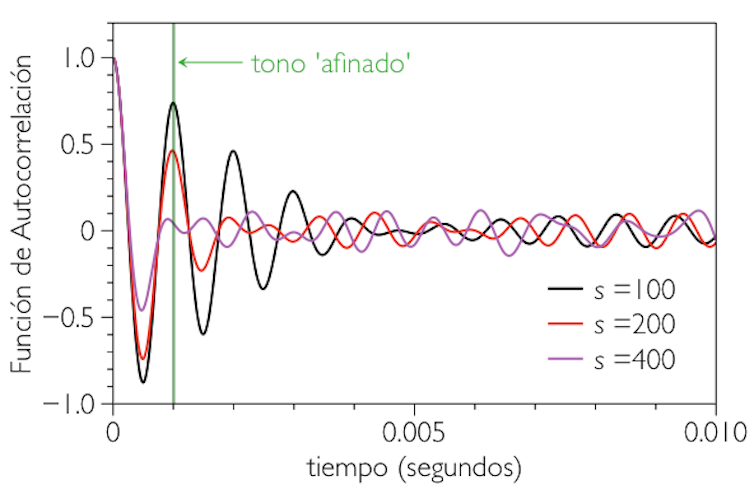
El resultado es el mismo si utilizamos simulaciones numéricas como las de la figura. El tono percibido (primer pico de la función de autocorrelación) coincide con el tono afinado siempre que la varianza no sea excesivamente grande.

Como la varianza es baja porque todo el público del concierto canta la misma canción a la vez, entonces poco importa que cantemos todos mal. Si somos muchos, el público cantará genial.
Lucas Lacasa, Doctor en Física y Profesor de Matemática Aplicada en Queen Mary University of London, Queen Mary University of London
Este artículo fue publicado originalmente en The Conversation. Lea el original.
--
--




